Today, my friends and I got to talking about the age of the human race under both Evolutionary and Biblical timelines. In particular there was the question of whether or not the roughly 6,000 years of Biblical history allow sufficient time for the human population to grow from 2 to approximately 7 billion. I was curious about this and did some back of the envelope calculations along with some SWAGs (emphasis on the 'WA').
For the population model I assumed that 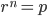 where
where 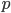 is the current population,
is the current population,  is the number of generations since Adam and Eve were banished from the garden, and
is the number of generations since Adam and Eve were banished from the garden, and  is the average rate of children produced per parent that go on to produce children of their own. First, I assumed that
is the average rate of children produced per parent that go on to produce children of their own. First, I assumed that  would be something like 1.5, since people have historically had big families but things like war, plague, and famine substantially decrease the number of offspring that have children of their own. Finally,
would be something like 1.5, since people have historically had big families but things like war, plague, and famine substantially decrease the number of offspring that have children of their own. Finally,  is the number of generations. Typing this into wolfram alpha as log(1.5, 7000000000) results in just under 56 generations which doesn't seem like that long. If one assumes that the average age of child birth is 25, then that results in 1,400 years. More than enough time to achieve the current population.
is the number of generations. Typing this into wolfram alpha as log(1.5, 7000000000) results in just under 56 generations which doesn't seem like that long. If one assumes that the average age of child birth is 25, then that results in 1,400 years. More than enough time to achieve the current population.
What if we take 25 and plug it into a model based on the Evolution timeline? According to wikipedia, the current iteration of humanity, also known as homo sapiens sapiens, has been around for about 200,000 years and that would mean about 8,000 generations. Although I haven't had any life sciences education since highschool, that seems like a plausible number of generations within which to achieve the ethnic diversity currently present in humanity. Anyway plugging these numbers back into our model, we want to solve 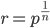 , we can type 7000000000^(1/8000) into wolfram alpha giving us about 1.003.
, we can type 7000000000^(1/8000) into wolfram alpha giving us about 1.003.
This is an unsettlingly low number for  , but it seems plausible to me. For centuries, life for people has been, as Thomas Hobbes used to say, "nasty, brutish, and short".
, but it seems plausible to me. For centuries, life for people has been, as Thomas Hobbes used to say, "nasty, brutish, and short".
I will do my best to make future blog posts for the new year more cheerful :-).
