I recently entered a submission to the Kaggle digit recognition contest based on the scikit-learn implementation of the k-nearest neighbor algorithm which resulted in a modest 96.6% accuracy. Hastie et. al. define this algorithm as:

$$\hat{Y}\left(x\right)=\frac{1}{k}\sum\limits_{x_i \in N_k\left(x\right)}y_i$$

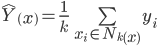
This simply says that we are looking at all of the training samples within a neighborhood and averaging their values to determine an estimate, $\hat{Y}$ for a test sample in question. I arbitrarily chose  a neighborhood size of 10 and the default Minkowski distance with p=2 (Euclidean) as follows:

Execution took about 20 minutes and 53 seconds my computer's 3.4 GHz i7 processor: quite a bit of time, but perhaps not surprising as k-NN is sometimes referred to as a "Lazy Learner". In other words, it postpones generalization until the actual query is made. In this case, there are 28,000 such queries and 784 dimensions per neighbor in each query (one dimension per pixel) so that's a lot of computation to delay!

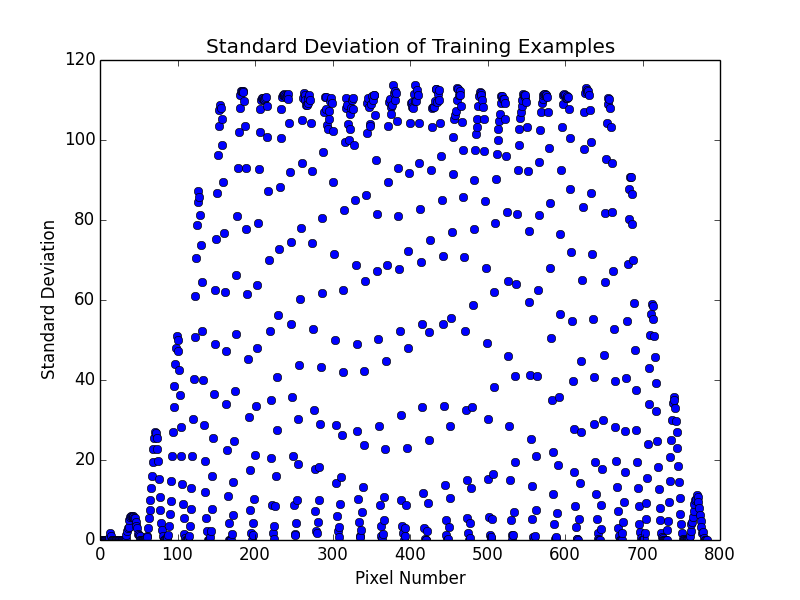
Obviously, the sensible approach in this case would be to find some way to reduce the number of dimensions if possible.  One can look at the amount of information that each pixel encodes in the training examples. Looking around the web, I found one article on this same problem and so, I attempted to follow the author's Exploratory Data Analysis technique by looking at the standard deviation and Coefficient of Variation across pixels within the training examples using the following python code:

Plotting the standard deviation gave the following result which matched the original author's work nicely:

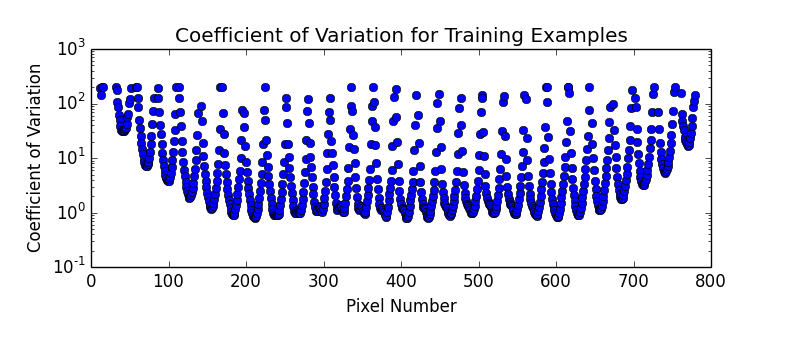
And then calculating CoV:

produced the following plot:

Whoa! That doesn't look right at all. Or does it? It turns out that quite a few of the pixels have means close to zero which result in rather large numbers for something that should be a normalized quantity. Let's look at the same data plotted with a logarithmic y axis:

Well that's a bit easier to make sense of. Unfortunately though, it doesn't seem like CoV is a very good statistic to use for our purposes here because so many of the values are large. I plan to return soon with more results!