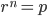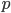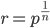It is said that when Hernando Cortes landed in the Yucatan with only 600 men to confront the full might of the Aztec empire he made the radical decision to burn the ships of his fleet, removing any possibility of retreat or return to home save by acquiring new ships as spoils of war. It's hard to overstate the motivation one experiences when failure is no longer an option and this is something I feel like I can say I've truly experienced in recent months.
The comfort and security of the familiar is like a warm campfire that lulls us to sleep. Then, later... perhaps much later, like the gunslinger in Stephen King's novels, we awaken to find the campfire has long since died out, we are much older than before, and lost in a strange new world.
But good or bad, change is the agent that restores our awareness. It brings color and vividness to our lives. It challenges us to grow, to become more than what we would be otherwise. As Frank Herbert wrote, "Without change something sleeps inside us and seldom awakens. The sleeper must awaken!" I believe the sleeper he was referring to is the mythical hero inside ourselves. It's the hero that Joseph Campbell wrote about. The hero that calls us on a journey away from the comfortable and familiar.
I feel like my own journey is beginning once again. No doubt there will be many adventures to come. I am truly thankful to all my friends. I hope you know who you are.
With that, I leave you with this song that to me evokes the spirit of the mythical hero.