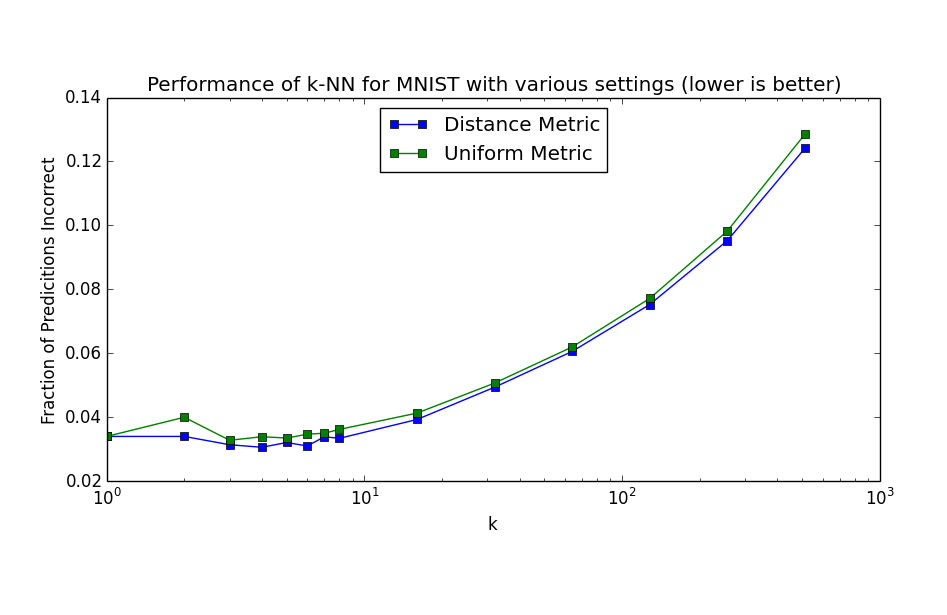
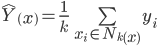I decided to try a few more things with k-NN on the MNIST data, namely varying k and trying the same settings of k for both distance and uniform metrics. For each experiment, I used k-fold cross validation with 5 folds. It turned out that setting k=6 with distance metric gave the best overall performance at just a smidgen under a respectable 97% accuracy (96.957% to be exact). The results of testing the various settings are shown in the plot below.
It's interesting to compare this plot to a similar plot on page 17 of Hastie et al. As expected, performance degrades with increasing k beyond 10 or so. However, there is no corresponding degradation with very low k, which would be a result of overfitting. My guess is that overfitting is happening, but isn't noticeable in this plot because the Curse of Dimensionality is preventing the "sweet spot" (which I would guess is in the k=4-8 range) from maximizing its effectiveness.
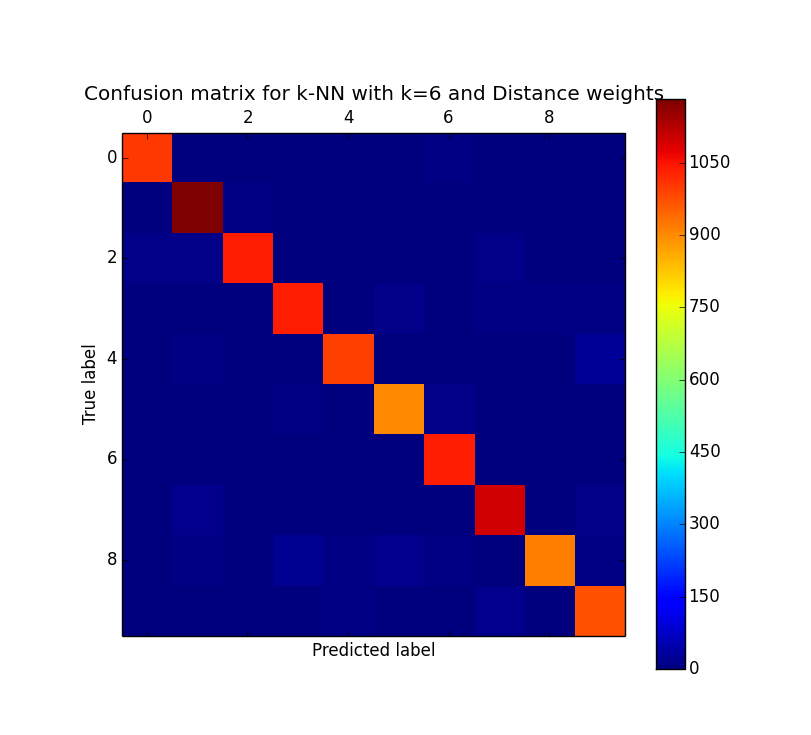
On a side note, its also interesting to look at the confusion matrix resulting from one of these experiments. For those not familiar, a confusion matrix simply plots predicted labels (in our case the digits 0-9) vs. actual labels. That is, what the algorithm thought something was, versus what it actually is. As shown below, the algorithm correctly predicted '1' almost all of the time while it had a bit more trouble with the digits 5 and 8.
In a future post, I'm planning to explore some dimensionality reduction techniques to see if it's possible to squeeze even more performance out of k-NN!