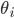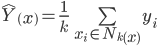In the science fiction novel Dune, the author, Frank Herbert describes a means of space travel called "folding space". The idea is that instead of trying to travel faster than light, you could bend 3-dimensional space into a 4th or higher dimension and appear wherever you wanted to go without actually moving. The people that do this sort of thing in the book are highly trained and intelligent because folding space is very dangerous.
Like the imaginary travel in Dune, machine learning poses its own set of dangers when confronted by high dimensions. This is known as the Curse of Dimensionality and it is regarded as the second biggest challenge in ML after overfitting.
So why is this such a problem? Because as we increase the number of variables, and hence dimensions, the amount of data required to effectively train a learner grows exponentially. To convince you that this is true, I'll start with a brief informal discussion, followed by an empirical treatment with one of my favorite tools, the R programming language. For a formal, mathematical treatment, I refer you to a beautiful paper by Mario Koppen. What I aim to do here though is hopefully introduce the topic in a slightly more approachable way for those from a computer science background like myself.
The first thing to consider is the vastness of high dimensional spaces. Just as there are an infinite number of planes that fill a cube, so too there are an infinite number of cubes that fill a hypercube. This is problem of size makes sense intuitively and by itself might seem to explain the need for a lot more data in high dimensions. Size isn't the only thing going on though. We have to understand how the locations of points in a hypercube relative to one another change with increasing dimensions. To understand these relationships we need to first think about how volumes change when moving from 3 to 4 dimensions and higher.
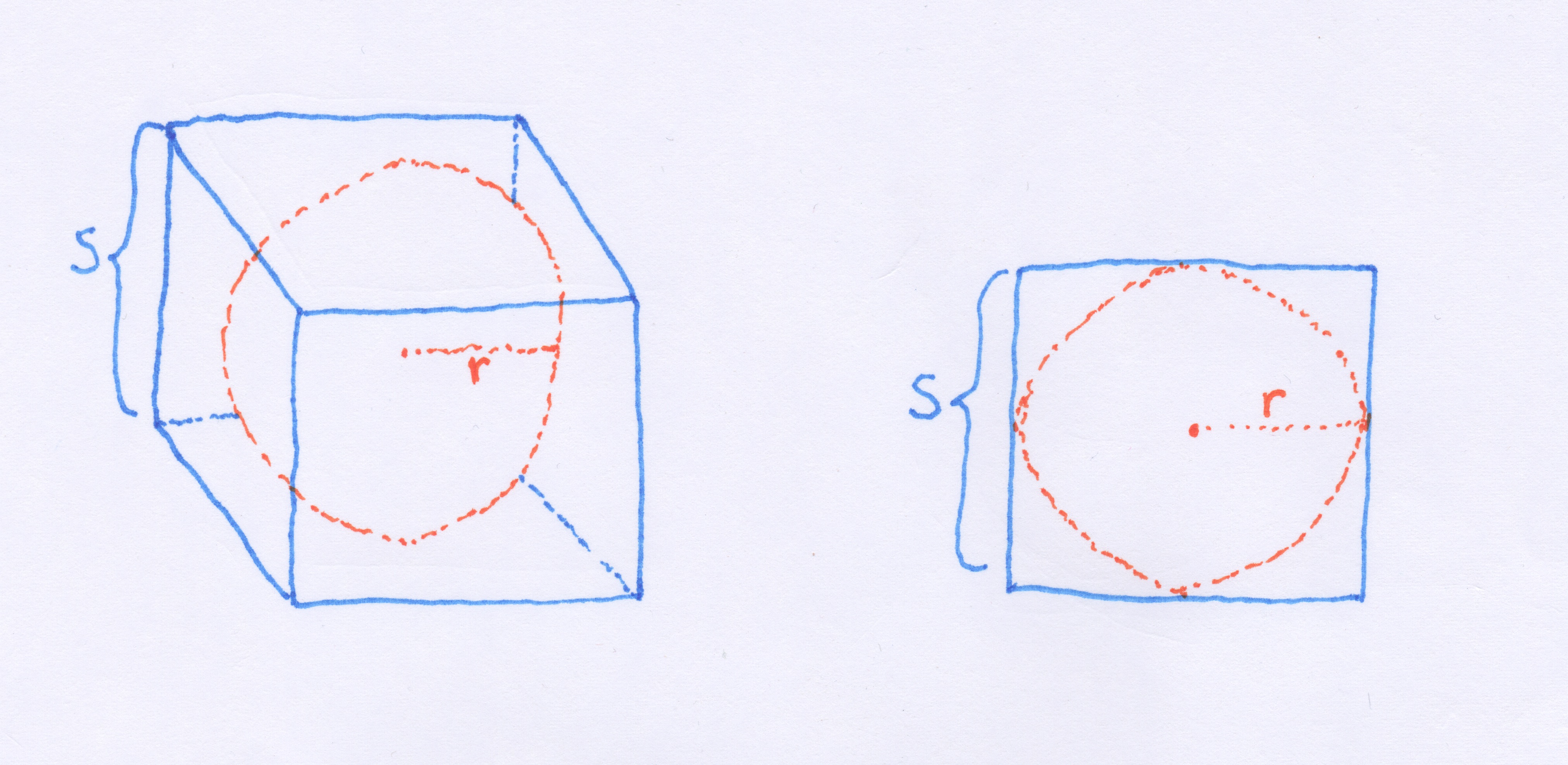
Let's consider what happens to the ratio of the volumes of an n-ball and an n-cube as we increase the number of dimensions. Above and on the left, I've drawn a sphere inscribed in a cube such that each side of the cube touches the ball. The ball's radius,  is one-half the width of the cube,
is one-half the width of the cube,  . Assuming a unit cube with
. Assuming a unit cube with  then with the equation for the volume of a sphere,
then with the equation for the volume of a sphere,  we get a volume of 0.524 for the inscribed sphere.
we get a volume of 0.524 for the inscribed sphere.
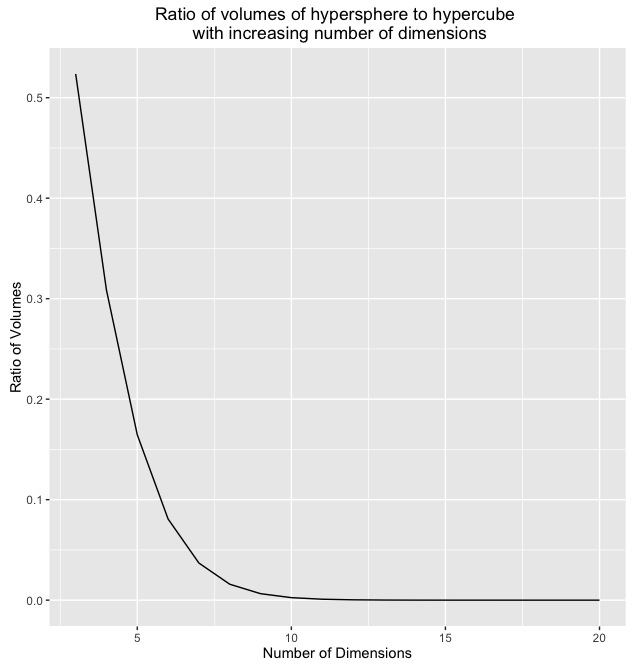
We might be tempted to think that this ratio would stay the same as the number of dimensions,  , increases, but we would be wrong. To demonstrate let's look at some R code:
, increases, but we would be wrong. To demonstrate let's look at some R code:
This computes the volume of a hypersphere for any number of dimensions and radius. If we run this code for different values of  and
and  and plot the results we get the following:
and plot the results we get the following:
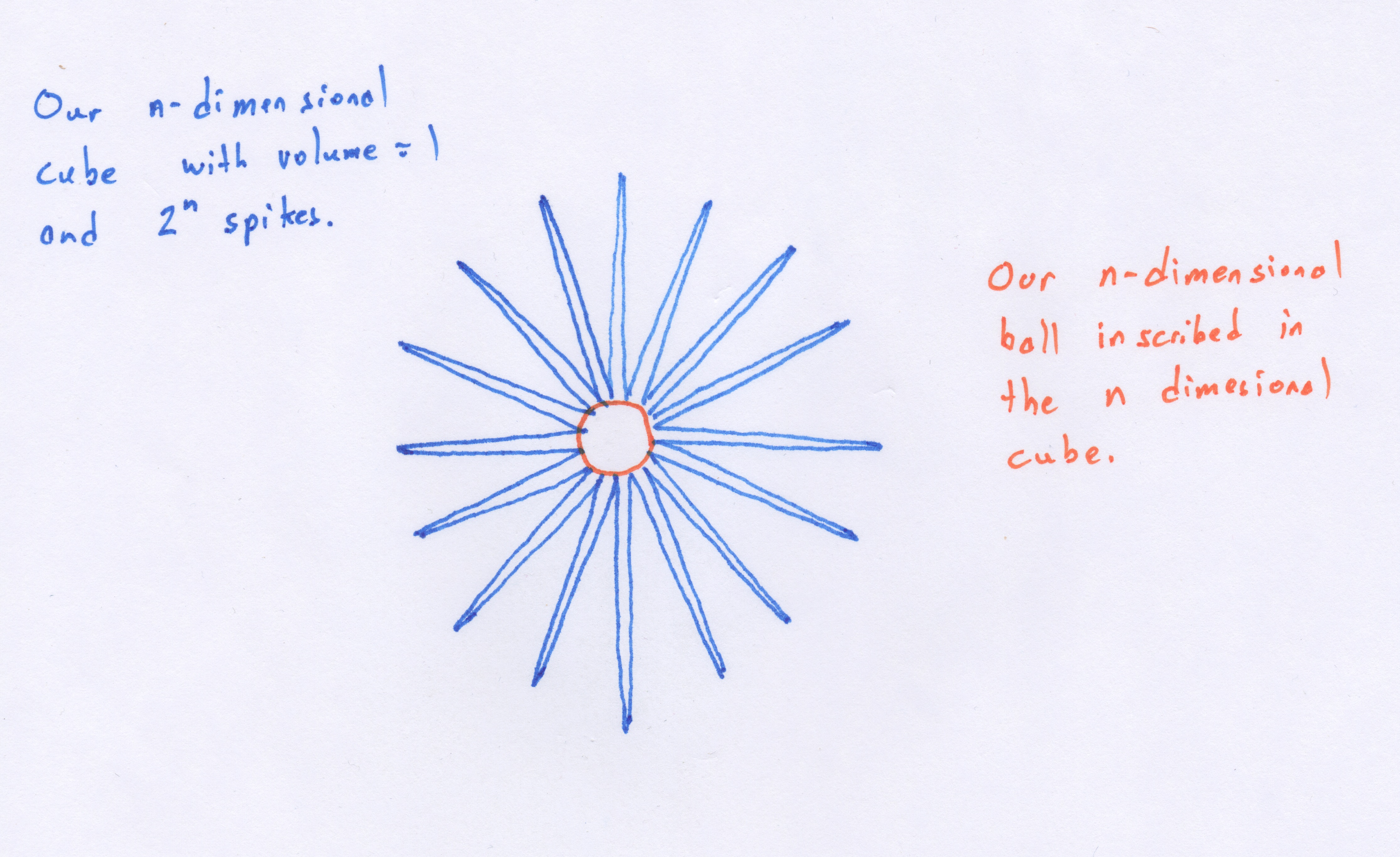
Wow! So the volume of the hypersphere becomes infinitely small while the volume of the hypercube with  remains constant. If we could somehow visualize what this situation looks like in high dimensions we would see what Koppen referred to as a "spiking hypercube" with the corners of the cube extending further and further away from the center which gets increasingly smaller. This means that with increasing dimensions, our data will almost never fall within the center of the volume. It will almost always be near the edges!
remains constant. If we could somehow visualize what this situation looks like in high dimensions we would see what Koppen referred to as a "spiking hypercube" with the corners of the cube extending further and further away from the center which gets increasingly smaller. This means that with increasing dimensions, our data will almost never fall within the center of the volume. It will almost always be near the edges!
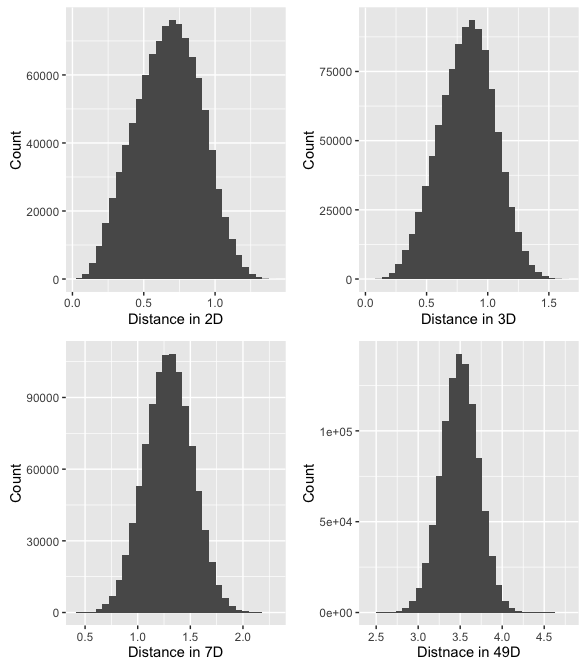
Another problem is that the distribution of distances between randomly chosen points in the volume begins to change. We can simulate this with the following bit of R code:
Running this code for a few different settings of n, with 1000 samples each generates the following histograms:
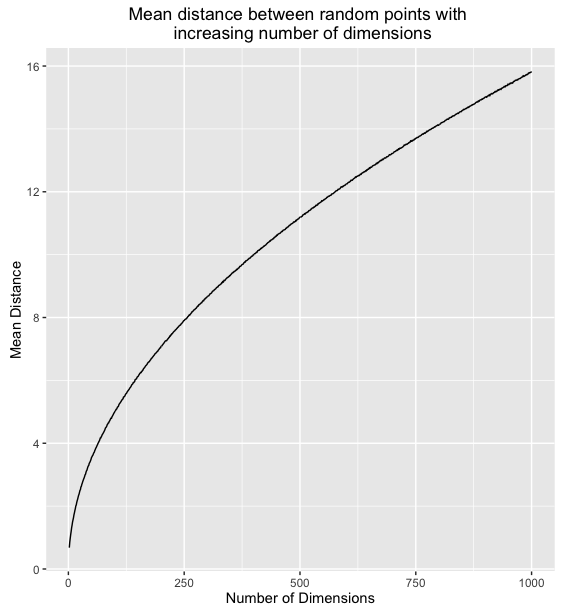
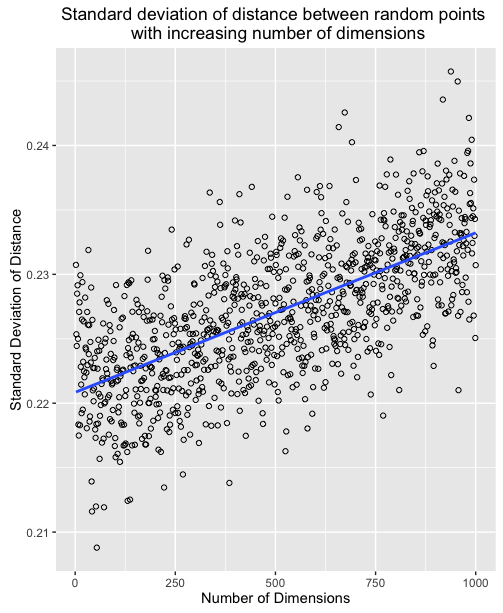
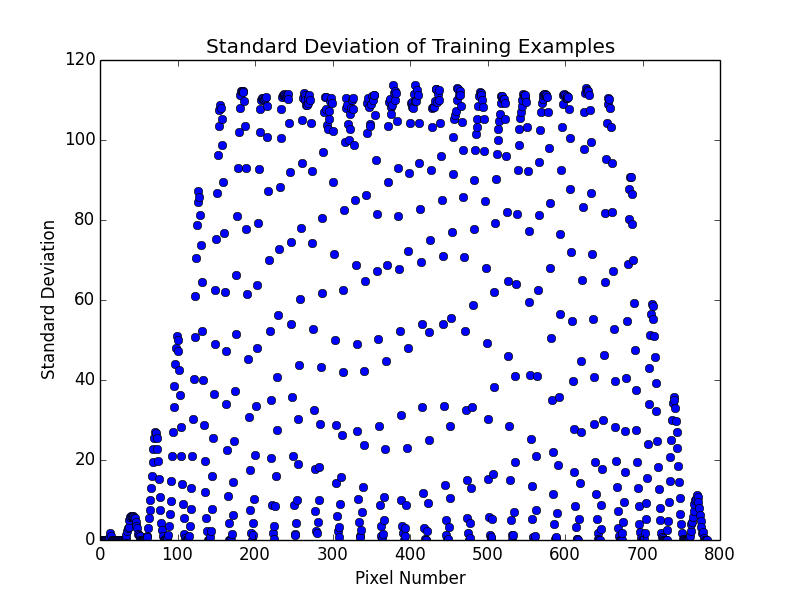
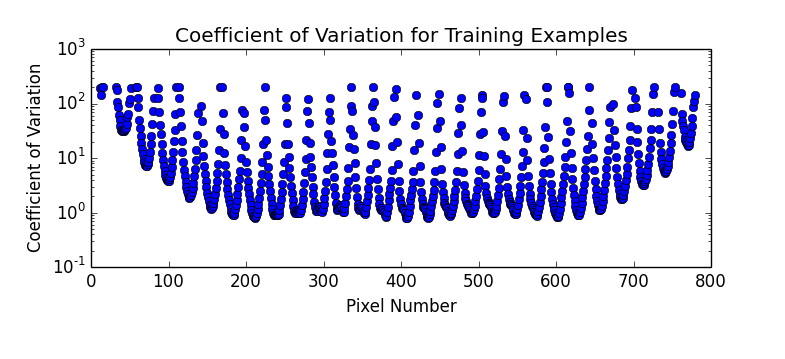
What's happening here, is that as the number of dimensions increases, the variance of the distances around a mean remains relatively unchanged even though the mean itself is increasing. To further illustrate we can plot the mean and standard deviation of distance for 1000 sample points for all number of dimensions between 2 and 1000.
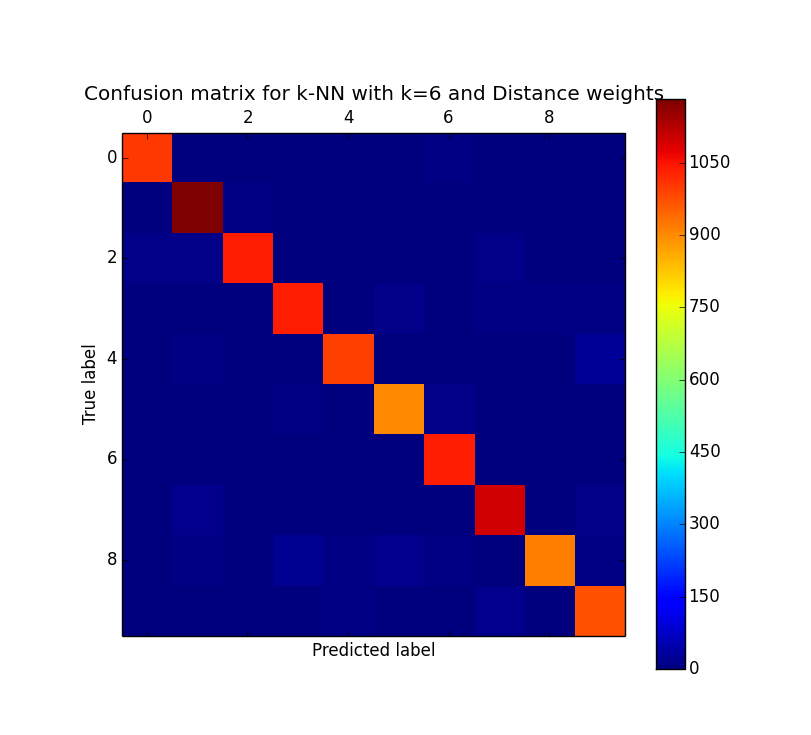
This means that in high dimensions, other points will tend to be clustered at similar distances from any other point. This is why instance based methods, like knn tend to have difficulty in high dimensions. As the number of dimensions increases, the distance to other points becomes increasingly similar until the choice of the k nearest points becomes random.
Well, I hope this brief post helped you understand this very important challenge in ML. I feel like writing it helped improve my own understanding. If this topic interests you, I would definitely encourage you to read the papers by Koppen and Domingos that I linked to previously as they give a much more formal and authoritative treatment . You can find the complete source code to reproduce these experiments here.